|
Analysis of Potential Flows through Complex Variables
The properties exhibited by the velocity potential and stream function of two dimensional irrotational flow of an inviscid fluid are identical to those exhibited by the real and imaginary part of an analytic function of a complex variable. It is natural to combine 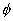 and and 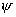 into an analytic function of a complex variable into an analytic function of a complex variable 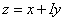 in the region of z plane occupied by the flow. Here, in the region of z plane occupied by the flow. Here, 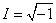 is called imaginary unit. is called imaginary unit.
| An analytic function, |
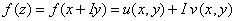 |
(22.11) |
| and |
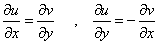 |
(22.12) |
These are known as Cauchy-Riemann condition. Also, 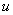 and and 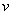 are real single valued continuous functions. We get from the above are real single valued continuous functions. We get from the above
| |
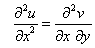 and and 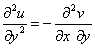 |
| Therefore, |
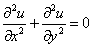 and and 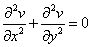 |
| Consider |
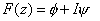 |
(22.13) |
where 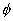 is velocity potential function and is velocity potential function and 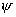 is stream function. This leads to is stream function. This leads to
| |
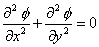 and and 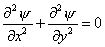 |
which means
| |
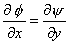 and and 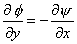 |
Finally we get
| |
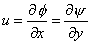 and and 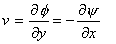 |
|
This completes the definition
| |
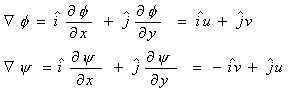 |
(22.14) |
| Also, |
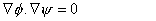 |
(22.15) |
Therefore 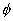 and and 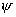 are perpendicular to each other. are perpendicular to each other.
Let us consider another function or complex potential
| Which gives, |
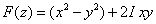 |
(22.16) |
Therefore, we get
| |
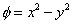 and and 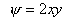 |
|
| |
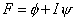 and and 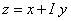 |
|
| |
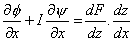 ; which means ; which means |
|
| |
 and and 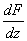 is the complex velocity is the complex velocity |
|
Therefore,
| |
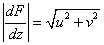 |
(22.17) |
|