|
Dimensions of Physical Quantities
All physical quantities are expressed by magnitudes and units.
For example , the velocity and acceleration of a fluid particle are 8m/s and 10m/s2 respectively. Here the dimensions of velocity and acceleration are ms-1 and ms-2 respectively.
In SI (System International) units, the primary physical quantities which are assigned base dimensions are the mass, length, time, temperature, current and luminous intensity. Of these, the first four are used in fluid mechanics and they are symbolized as M (mass), L (length), T (time), and θ (temperature).
-
Any physical quantity can be expressed in terms of these primary quantities by using the basic mathematical definition of the quantity.
-
The resulting expression is known as the dimension of the quantity.
Let us take some examples:
- Dimension of Stress
Shear stress
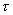 is defined as force/area. Again, force = mass × acceleration is defined as force/area. Again, force = mass × acceleration
Dimensions of acceleration = Dimensions of velocity/Dimension of time.

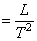
Dimension of area = (Length)2 =L2
Hence, dimension of shear stress
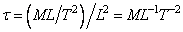 |
(19.1) |
- Dimension of Viscosity
Consider Newton's law for the definition of viscosity as
or,
The dimension of velocity gradient du/dy can be written as
dimension of du/dy= dimension of u/dimension of y = (L / T)/L = T -1
The dimension of shear stress 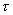 is given in Eq. (19.1). is given in Eq. (19.1).
Hence dimension of
|