|
Losses Due to Sudden Enlargement
- If the cross-section of a pipe with fluid
flowing through it, is abruptly enlarged (Fig. 14.2a) at
certain place, fluid emerging from the smaller pipe is unable
to follow the abrupt deviation of the boundary.
- The streamline takes a typical diverging
pattern (shown in Fig. 14.2a). This creates pockets of
turbulent eddies in the corners resulting in the dissipation
of mechanical energy into intermolecular energy.
Basic mechanism
of this type of loss
- The fluid flows against an adverse pressure
gradient. The upstream pressure p1 at section
a-b is lower than the downstream pressure p2
at section e-f since the upstream velocity V1
is higher than the downstream velocity V2 as
a consequence of continuity.
- The fluid particles near the wall due
to their low kinetic energy cannot overcome the adverse
pressure hill in the direction of flow and hence follow
up the reverse path under the favourable pressure gradient
(from p2 to p1).
- This creates a zone of recirculating
flow with turbulent eddies near the wall of the larger tube
at the abrupt change of cross-section, as shown in Fig.
14.2a, resulting in a loss of total mechanical energy.
- For high values of Reynolds number, usually
found in practice, the velocity in the smaller pipe may
be assumed sensibly uniform over the crosssection. Due to
the vigorous mixing caused by the turbulence, the velocity
becomes again uniform at a far downstream section e-f from
the enlargement (approximately 8 times the larger diameter).
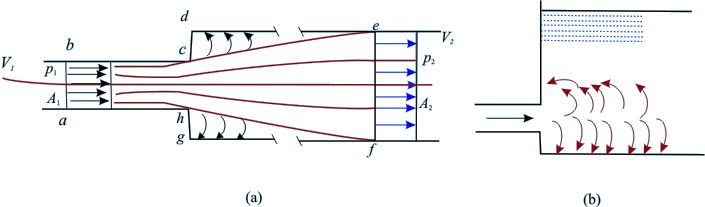
Fig 14.2 (a) Flow
through abrupt but finite enlargement
(b) Flow at Infinite enlargement (Exit
Loss)
- A control volume abcdefgh is considered
(Fig. 14.2a) for which the momentum theorem can be written
as
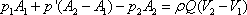 |
(14.20) |
where A1, A2 are the cross-sectional areas of the smaller and larger parts
of the pipe respectively, Q is the volumetric fllow rate and p’ is the mean
pressure of the eddying fluid over the annular face, gd. It is known from
experimental evidence, the p’ = p1.
- Hence the Eq. (14.20) becomes
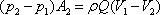 |
(14.21) |
- From the equation of continuity
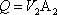 |
(14.22) |
- With the help of Eq. (14.22), Eq. (14.21)
becomes
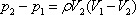 |
(14.23) |
- Applying Bernoulli's equation
between sections ab and ef in consideration of the flow
to be incompressible and the axis of the pipe to be horizontal,
we can write
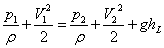
|
|
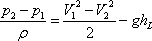 |
(14.24) |
where hL is the
loss of head. Substituting (p2 −p1)
from Eq. (14.23) into Eq. (14.24), we obtain
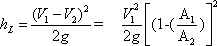 |
(14.25) |
- In view of the assumptions made, Eq.(14.25)
is subjected to some inaccuracies, but experiments show
that for coaxial pipes they are within only a few per cent
of the actual values.
Back to original slide - "Losses due to geometric changes"
Exit Loss
- If, in Eq.(14.25),
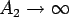 ,
then the head loss at an abrupt enlargement tends to ,
then the head loss at an abrupt enlargement tends to 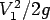 . The
physical resemblance of this situation is the submerged
outlet of a pipe discharging into a large reservoir as shown
in Fig.14.2b. . The
physical resemblance of this situation is the submerged
outlet of a pipe discharging into a large reservoir as shown
in Fig.14.2b.
- Since the fluid velocities are arrested
in the large reservoir, the entire kinetic energy at the
outlet of the pipe is dissipated into intermolecular energy
of the reservoir through the creation of turbulent eddies.
- In such circumstances, the loss is usually
termed as the exit loss for the pipe and
equals to the velocity head at the discharge end of the
pipe.
Back to original slide - "Losses due to geometric changes"
|