|
Forced Vortex Flows
- Flows where streamlines are concentric
circles and the tangential velocity is directly proportional
to the radius of curvature are known as plane
circular forced vortex flows.
- The flow field is described in a polar
coordinate system as,
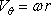
|
(14.17a) |
and 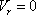 |
(14.17b) |
- All fluid particles rotate with the
same angular velocity ω like a solid body. Hence a
forced vortex flow is termed as a solid body rotation.
- The vorticity Ω for the flow field
can be calculated as
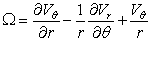
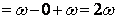
- Therefore, a forced vortex motion is
not irrotational; rather it is a rotational flow with a
constant vorticity 2ω. Equation (14.8) is used to
determine the distribution of mechanical energy across the
radius as
- Integrating the equation between the two radii on the same horizontal plane,
we have,
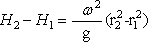 |
(14.18) |
- Thus, we see from Eq. (14.18) that the
total head (total energy per unit weight) increases with
an increase in radius. The total mechanical energy at any
point is the sum of kinetic energy, flow work or pressure
energy, and the potential energy.
- Therefore the difference in total head
between any two points in the same horizontal plane can
be written as,
- Substituting this expression of H2-H1
in Eq. (14.18), we get
- The same equation can also be obtained
by integrating the equation of motion in a radial direction
as
- To maintain a forced vortex flow, mechanical
energy has to be spent from outside and thus an external
torque is always necessary to be applied continuously.
- Forced vortex can be generated by rotating
a vessel containing a fluid so that the angular velocity
is the same at all points.
|
|
|