Viscosity ( μ ) :

• Newton postulated that τ is proportional to the quantity Δu/ Δy where Δy  is the distance of separation of the two layers and Δu  is  the difference in their velocities.
  
  

• In the limiting case of , Δu / Δy equals du/dy, the velocity gradient at a point in a direction perpendicular to the direction of the motion of the layer.
  
  

• According to Newton τ and du/dy bears the relation
  

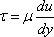(1.7)

where, the constant of proportionality μ is known as the coefficient of viscosity or simply viscosity which is a property of the fluid and depends on its state. Sign of τ depends upon the sign of du/dy. For the profile shown in Fig. 1.5, du/dy is positive everywhere and hence, τ is positive. Both the velocity and stress are considered positive in the positive direction of the coordinate parallel to them.
Equation

defining the viscosity of a fluid, is known as Newton's law of viscosity. Common fluids, viz. water, air, mercury obey Newton's law of viscosity and are known as Newtonian fluids.

Other classes of fluids, viz. paints, different polymer solution, blood do not obey the typical linear relationship, of τ and du/dy and are known as non-Newtonian fluids. In non-newtonian fluids viscosity itself may be a function of deformation rate as you will study in the next lecture.