Figure 37.3 H-Q Characteristics of pump and system |
Effect of Speed Variation
Head-Discharge characteristic of a given pump is always referred to a constant speed. If such characteristic at one speed is know, it is possible to predict the characteristic at other speeds by using the principle of similarity. Let A, B, C are three points on the characteristic curve (Fig. 37.4) at speed 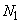 . .
For points A, B and C , the corresponding heads and flows at a new speed 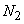 are found as follows: are found as follows:
Figure 37.4 Effect of speed variation on operating point of a centrifugal pump |
From the equality of 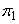 term [Eq. (3.1)] gives term [Eq. (3.1)] gives
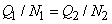 |
(since for a given pump D is constant) |
(37.6) |
and similarly, equality of 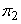 term [Eq. (3.1)] gives term [Eq. (3.1)] gives
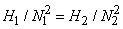 |
(37.7) |
Applying Eqs. (37.6) and (37.7) to points A, B and C the corresponding points 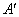 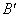 and and 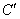 are found and then the characteristic curve can be drawn at the new speed are found and then the characteristic curve can be drawn at the new speed 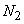
Thus,
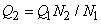 and and
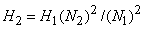 |
which gives
Equation (37.8) implies that all corresponding or similar points on Head-Discharge characteristic curves at different speeds lie on a parabola passing through the origin. If the static lift 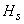 becomes zero, then the curve for system characteristic and the locus of similar operating points will be the same parabola passing through the origin. This means that, in case of zero static life, for an operating point at speed becomes zero, then the curve for system characteristic and the locus of similar operating points will be the same parabola passing through the origin. This means that, in case of zero static life, for an operating point at speed 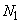 , it is only necessary to apply the similarity laws directly to find the corresponding operating point at the new speed since it will lie on the system curve itself (Figure 37.4). , it is only necessary to apply the similarity laws directly to find the corresponding operating point at the new speed since it will lie on the system curve itself (Figure 37.4).
|