As the impeller rotates, the fluid is drawn into the blade passage at the impeller eye, the centre of the impeller. The inlet pipe is axial and therefore fluid enters the impeller with very little whirl or tangential component of velocity and flows outwards in the direction of the blades. The fluid receives energy from the impeller while flowing through it and is discharged with increased pressure and velocity into the casing. To convert the kinetic energy or fluid at the impeller outlet gradually into pressure energy, diffuser blades mounted on a diffuser ring are used.
The stationary blade passages so formed have an increasing cross-sectional area which reduces the flow velocity and hence increases the static pressure of the fluid. Finally, the fluid moves from the diffuser blades into the volute casing which is a passage of gradually increasing cross-section and also serves to reduce the velocity of fluid and to convert some of the velocity head into static head. Sometimes pumps have only volute casing without any diffuser.
Figure 34.1 shows an impeller of a centrifugal pump with the velocity triangles drawn at inlet and outlet. The blades are curved between the inlet and outlet radius. A particle of fluid moves along the broken curve shown in Figure 34.1.
Figure 34.1 Velocity triangles for centrifugal pump Impeller |
Let 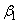 be the angle made by the blade at inlet, with the tangent to the inlet radius, while be the angle made by the blade at inlet, with the tangent to the inlet radius, while 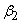 is the blade angle with the tangent at outlet. is the blade angle with the tangent at outlet. 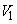 and and 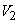 are the absolute velocities of fluid at inlet an outlet respectively, while are the absolute velocities of fluid at inlet an outlet respectively, while
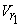 and and
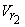 are the relative velocities (with respect to blade velocity) at inlet and outlet respectively. Therefore, are the relative velocities (with respect to blade velocity) at inlet and outlet respectively. Therefore,
Work done on the fluid per unit weight =
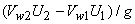 |
(34.1) |
A centrifugal pump rarely has any sort of guide vanes at inlet. The fluid therefore approaches the impeller without appreciable whirl and so the inlet angle of the blades is designed to produce a right-angled velocity triangle at inlet (as shown in Fig. 34.1). At conditions other than those for which the impeller was designed, the direction of relative velocity 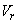 does not coincide with that of a blade. Consequently, the fluid changes direction abruptly on entering the impeller. In addition, the eddies give rise to some back flow into the inlet pipe, thus causing fluid to have some whirl before entering the impeller. However, considering the operation under design conditions, the inlet whirl velocity does not coincide with that of a blade. Consequently, the fluid changes direction abruptly on entering the impeller. In addition, the eddies give rise to some back flow into the inlet pipe, thus causing fluid to have some whirl before entering the impeller. However, considering the operation under design conditions, the inlet whirl velocity 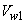 and accordingly the inlet angular momentum of the fluid entering the impeller is set to zero. Therefore, Eq. (34.1) can be written as and accordingly the inlet angular momentum of the fluid entering the impeller is set to zero. Therefore, Eq. (34.1) can be written as
Work done on the fluid per unit weight =
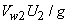 |
(34.2) |
We see from this equation that the work done is independent of the inlet radius. The difference in total head across the pump known as manometric head, is always less than the quantity
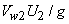 because of the energy dissipated in eddies due to friction. because of the energy dissipated in eddies due to friction.
The ratio of manometric head H and the work head imparted by the rotor on the fluid
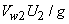 (usually known as Euler head) is termed as manometric efficiency (usually known as Euler head) is termed as manometric efficiency 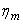 . It represents the effectiveness of the pump in increasing the total energy of the fluid from the energy given to it by the impeller. Therefore, we can write . It represents the effectiveness of the pump in increasing the total energy of the fluid from the energy given to it by the impeller. Therefore, we can write
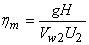 |
(34.3) |
The overall efficiency  of a pump is defined as of a pump is defined as
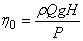 |
(34.4) |
where, Q is the volume flow rate of the fluid through the pump, and P is the shaft power, i.e. the input power to the shaft. The energy required at the shaft exceeds
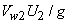 because of friction in the bearings and other mechanical parts. Thus a mechanical efficiency is defined as because of friction in the bearings and other mechanical parts. Thus a mechanical efficiency is defined as
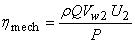 |
(34.5) |
so that
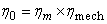 |
(34.6) |
|