Reaction Turbine, Continued
Put 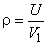 then then
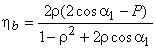 |
(25.1) |
For the maximum efficiency 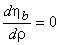 and we get and we get
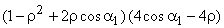 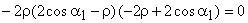 |
(25.2) |
from which finally it yields
Figure 25.1 Velocity diagram for maximum efficiency
Absolute velocity of the outlet
at this stage is axial (see figure 25.1). In this
case, the energy transfer
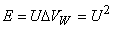 |
(25.4) |
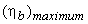 can be found out by putting the value of can be found out by putting the value of 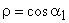 in the expression for blade efficiency in the expression for blade efficiency
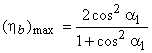 |
(25.5) |
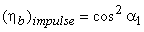 |
(25.6) |
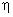 is greater in reaction turbine. Energy input per stage is less, so there are more number of stages. is greater in reaction turbine. Energy input per stage is less, so there are more number of stages.
Stage Efficiency and Reheat factor
The Thermodynamic effect on the turbine
efficiency can be best understood by considering a
number of stages between two stages 1 and 2 as shown
in Figure 25.2
Figure 25.2 Different stage of a steam turbine
The total expansion is divided into four stages of the same efficiency 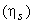 and pressure ratio. and pressure ratio.
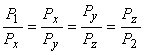 |
(25.7) |
The overall efficiency of expansion is 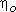 . The actual work during the expansion from 1 to 2 is . The actual work during the expansion from 1 to 2 is
Reheat factor (R.F.)= 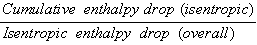
R.F is 1.03 to 1.04
If 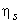 remains same for all the stages or remains same for all the stages or 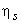 is the mean stage efficiency. is the mean stage efficiency.
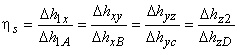 |
(25.10) |
or, 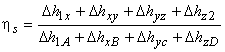 |
(25.11) |
We can see:
This makes the overall efficiency of the turbine greater than the individual stage efficiency.
The effect depicted by Eqn (25.12)
is due to the thermodynamic effect called "reheat".
This does not imply any heat transfer to the stages
from outside. It is merely the reappearance of stage
losses an increased enthalpy during the constant pressure
heating (or reheating) processes AX, BY, CZ and D2.
|