| |
Finite Element Equations for Piecewise Cubic Basis Functions
Finite element equations corresponding to the piecewise cubic basis functions are derived using the procedure similar to that of sections (8.3 - 8.6).
- First, the primary variable is approximated using the piecewise cubic basis functions
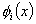 : :
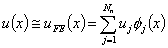 |
(8.38) |
Here, 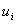 is the value of the primary variable at node ' i ' and Nn is the number of nodes. The quantities is the value of the primary variable at node ' i ' and Nn is the number of nodes. The quantities 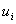 , i = 1, ., Nn are called as the degrees of freedom (abbreviated as dof). Note that, when piecewise cubic basis functions are used, the number of nodes ( Nn ) is equal to 3N +1, where N is the number of elements. , i = 1, ., Nn are called as the degrees of freedom (abbreviated as dof). Note that, when piecewise cubic basis functions are used, the number of nodes ( Nn ) is equal to 3N +1, where N is the number of elements.
- This approximation is substituted into the weighted residual integral (equation 8.19). For the Galerkin method, we substitute
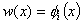 |
(8.39) |
and derive the expressions for the global stiffness matrix 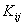 and the global force vector and the global force vector 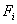 . From these expressions, the expressions for the element stiffness matrix . From these expressions, the expressions for the element stiffness matrix 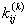 and the element force vector and the element force vector 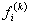 are extracted. This procedure is similar to that described in section 8.4. Note that, when piece wise cubic basis functions are used, there are 4 nodes per element and 4 shape functions per element. The shape functions are given by the expression (8.8) where p = 3 for the piecewise cubic basis functions. Thus, the size of are extracted. This procedure is similar to that described in section 8.4. Note that, when piece wise cubic basis functions are used, there are 4 nodes per element and 4 shape functions per element. The shape functions are given by the expression (8.8) where p = 3 for the piecewise cubic basis functions. Thus, the size of 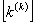 is 4X4 while that of is 4X4 while that of 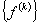 is 4x1. is 4x1.
- For each element, the element stiffness matrix
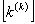 and the element force vector and the element force vector 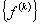 are calculated. are calculated.
- Then, the element stiffness matrices and the element force vectors are assembled over all the elements to form the global stiffness matrix [ K ] and the global force vector { F }. The assembly procedure is similar to that described in section 8.5
- Finally, the standard essential boundary condition (i.e., the Dirichlet boundary condition) is applied using the procedure similar to that of section 8.6.
|