Model Boundary Value Problem

To illustrate the development of integral formulations of the beam problem, we consider the cantilever beam shown in Fig. 18.1.

Figure 18.1 Model Boundary Value Problem

Length of the beam is L . The beam has a variable cross-section. The y-axis is the axis of symmetry of the cross-section. The variable moment of inertia of the cross section about z-axis is denoted by I(x). Young's modulus of the beam material is E . Since it is a cantilever beam, it is fixed at the end x = 0. The forces acting on the beam are : (i) (transverse) distributed force q (x) along y -axis and (ii) the shear force V along y -axis and the bending moment M about z -axis at the end x = L . Transverse displacement of a cross-section at x , denoted by 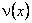, is governed by the following boundary value problem consisting of a differential equation (D.E.) and four boundary conditions (B.C) :

D.E.:		for	(18.1a)
B.C.:	(i)		(18.1b)
	(ii)		(18.1c)

The differential equation represents the force and moment equilibrium of a small element of the beam expressed in terms of 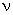using the stress-strain and strain-displacement relations. The important assumption made in deriving this equation is that the "plane cross-sections remain plane during the deformation". This assumption is strictly valid only for the case of pure bending, i.e., when there is no shear deformation. The boundary condition 1(b) is called as the Kinematic or the Dirichlet boundary condition where as the boundary condition 1(c) is called as the Force or the Neumann boundary condition. Next, we derive the integral formulations.