| |
Introduction
In the last three lectures, we discussed development of a one-dimensional finite element code. Even though we made certain simplifications about the variation of geometric, material and loading parameters, the algorithm of coding is sufficiently general and can easily be generalized to other variations of these parameters. In this lecture, we discuss the methods of testing a finite element code. In section 1, we discuss the patch test. In patch test, we select some problems for which the exact solution is a polynomial of degree p . We solve these problems using the FE code with one element and p -th order of approximation. If the nodal FE values do not match with the exact values, it means the code has certain errors. In section 2, we test the upper bound and mesh convergence of the FE solution. For this purpose, we choose a problem whose exact solution is not a polynomial. Let 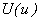 and and 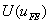 be the strain energies of the exact and FE solutions respectively. Note that, in Lecture 9, we showed that be the strain energies of the exact and FE solutions respectively. Note that, in Lecture 9, we showed that 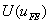 is always less than is always less than 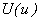 . Further, . Further, 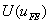 converges monotonically to converges monotonically to 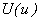 from below as the mesh is refined. If these trends are not exhibited by the FE solution obtained from the FE code, it means the code contains some errors. In section 3, we test the variation of the error norm from below as the mesh is refined. If these trends are not exhibited by the FE solution obtained from the FE code, it means the code contains some errors. In section 3, we test the variation of the error norm 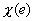 of the FE solution with mesh size h and order of approximation p . For this purpose, we choose the same problem as that of section 2. In Lecture 10, we showed that the natural logarithm of of the FE solution with mesh size h and order of approximation p . For this purpose, we choose the same problem as that of section 2. In Lecture 10, we showed that the natural logarithm of 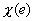 varies linearly with p and natural logarithm of h (eq. 10.13 or Fig. 10.1). If the FE solution obtained by the FE code does not show this variation, it means there are errors in the FE code. varies linearly with p and natural logarithm of h (eq. 10.13 or Fig. 10.1). If the FE solution obtained by the FE code does not show this variation, it means there are errors in the FE code. |