| |
Subroutine SHAPALL
Subroutine INTEG-PNTS of the previous section gives the values of the Gauss point coordinates 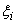 and the corresponding weights and the corresponding weights 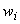 for given n (from 1 to 5). Subroutine SHAPE of section 11.5 calculates the values of shape functions and their derivatives for given for given n (from 1 to 5). Subroutine SHAPE of section 11.5 calculates the values of shape functions and their derivatives for given 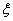 and given order of approximation p (from 1 to 3). Now we combine these two subroutines to generate the values of the shape functions and their derivatives at all the Gauss points for given n and given p . This is done through the subroutine SHAPALL. To simplify the calculation of n for given p , we make the choice that E is a constant, A is a linear functions of and given order of approximation p (from 1 to 3). Now we combine these two subroutines to generate the values of the shape functions and their derivatives at all the Gauss points for given n and given p . This is done through the subroutine SHAPALL. To simplify the calculation of n for given p , we make the choice that E is a constant, A is a linear functions of 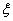 and f is a quadratic function of and f is a quadratic function of 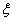 . Then . Then 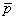 is given by equation (12.36) and n is found from inequality (12.29). We choose the minimum value of n . is given by equation (12.36) and n is found from inequality (12.29). We choose the minimum value of n .
We use the following notation for the variables.
- Scalar variables:
i,j : indices for do loop (integer)
n : number of Gauss points (integer)
ndofel : number of degrees of freedom per element (integer)
p : order of approximation (integer)
pbar : temporary variable (integer)
psi : natural coordinate
- Array variables:
dshap (ndofel) : values of the shape function derivates at given 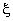 (real) (real)
dshaptot (n,ndofel) : values of the shape function derivatives at all the Gauss
points (real)
psi (n) : Gauss point coordinates (real)
shap (ndofel) : shape function values at given 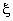 (real) (real)
shaptot (n,ndofel) : shape function values at all the Gauss points (real)
w (n) : weights corresponding to Gauss point coordinates (real)
- INPUT variable : p
- OUTPUT variables : n, psi, w, ndofel, shaptot, dshaptot
Now, the subroutine can be written as follows.
Subroutine SHAPALL (p, n, psi, w, ndofel, shaptot, dshaptot)
pbar = max (2p-1, p+2)
if pbar is odd
n = (pbar+1)/2
else
n = (pbar+2)/2
end if
call INTG-PNTS (n, psi, w)
do i = 1, n
psi = psi (i)
call SHAPE ( p, psi, ndofel, shap, dshap)
do j = 1, ndofel
shaptot ( i, j ) = shap (ndofel)
dshaptot ( i, j) = dshap (ndofel)
end do
end do
|