Mapping Fuction
Figure 11.1 shows a mapping of a typical element k (of p th order) to the master element. 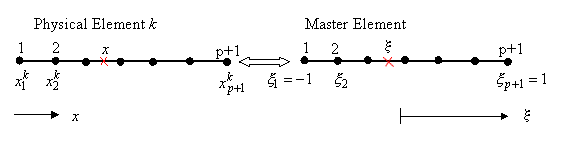
Fig 11.1 Mapping from physical element to master element
The figure also shows the local node numbering system on both the physical element and the master element. The local notation for x -coordinate of the nodes is shown on the physical element. The coordinate used for the master element is denoted by x . Over the master element, it varies from -1 to 1. It is called as the natural coordinate. The x - coordinate of the nodes is also indicated on the master element.
Note that, we wish to map a physical element of length 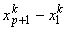 onto the master element of size two. Further the origin of the coordinate system on the master element is at its center. Thus, mapping of the physical element onto the master element involves the following : onto the master element of size two. Further the origin of the coordinate system on the master element is at its center. Thus, mapping of the physical element onto the master element involves the following :
- Translation of the physical element till its center coincides with the origin of the coordinate system.
- Stretching or compression of the element till its length becomes two.
This kind of mapping can always be expressed by the following linear relationship between x and 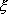 : :
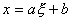 |
(11.1) |
where a and b are constants. This mapping is called as the linear or affine mapping. The constants a and b are determined from the condition that the end points of the physical element map onto the end points of the master element. Thus,
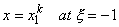 |
(11.2) |
and
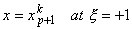 |
(11.3) |
Evaluating equation (11.1) at the points 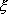 = -1 and = -1 and 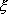 = 1 and using the conditions (11.2) and (11.3), we get = 1 and using the conditions (11.2) and (11.3), we get
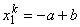 |
(11.4) |
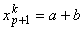 |
(11.5) |
Solution of these equations is
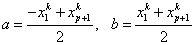 |
(11.6) |
Substituting the above expressions for a and b into equation (11.1) and rearranging the resulting equation, we get
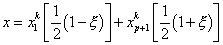 |
(11.7) |
This is the mapping function which maps a physical element of length 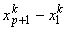 onto the master element. It is a relationship between the physical coordinate x and the natural coordinate onto the master element. It is a relationship between the physical coordinate x and the natural coordinate 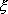 . .
|