Clausius Inequality
Consider a system undergoing a reversible cycle. The given cycle may be sub-divided by drawing a family of reversible adiabatic lines. Every two adjacent adiabatic lines may be joined by two reversible isotherms (refers to Figure 21.2)
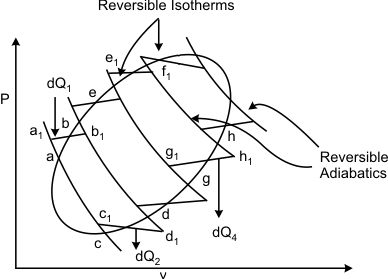
Figure 21.2
Now,
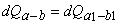 and and 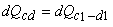 |
(21.5) |
Also, 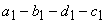 is a Carnot cycle which receives heat is a Carnot cycle which receives heat 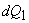 during the during the 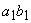 process and rejects heat process and rejects heat 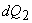 during the during the 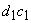 process. Let the heat addition be at temperature process. Let the heat addition be at temperature 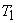 and the heat rejection be at temperature and the heat rejection be at temperature 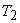 . Then it is possible to write, . Then it is possible to write,
and
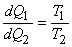 |
(21.6) |
or,
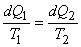 |
(21.7) |
Since 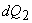 is negative, it reduces to is negative, it reduces to
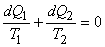 |
(21.8) |
Similarly for the cycle 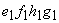
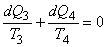 |
(21.9) |
If similar equations are written for all the elementary cycles, then
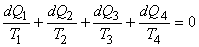 |
(21.10) |
or,
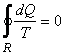 |
(21.11) |
Let us go back to the cycle 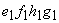
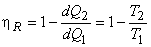 |
(21.12) |
Now 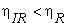 where, where, 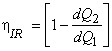 and this is not equal to and this is not equal to 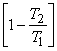 . .
For the irreversible cycle,
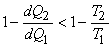 |
(21.13) |
or,
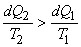 and and 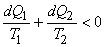 |
(21.14) |
because 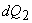 is negative. is negative.
Similarly, for the irreversible cycle 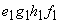
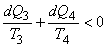 |
(21.15) |
Summing up all elementary cycles
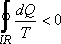 |
(21.16) |
The above two conclusions about reversible and irreversible cycles can be generalized as
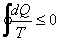 |
(21.17) |
The equality holds good for a reversible cycle and the inequality holds good for an irreversible cycles. The complete expression is known as Clausius Inequality.
|