Principle II:
All reversible heat engines operating between the two given thermal reservoirs have the same efficiency. The efficiency of reversible heat engine does not depend on the working fluid, it depends only on the temperature of the reservoirs between which it operates.
To prove the proposition, let us assume that the efficiency of the reversible engine 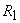 is greater than the efficiency of the reversible engine is greater than the efficiency of the reversible engine 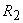 . .
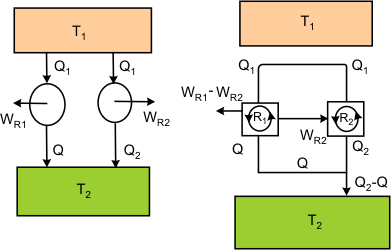
Figure 19.3
Refer to Figure 19.3. The engine 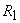 absorbs energy as heat absorbs energy as heat 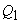 from the constant temperature thermal reservoir at from the constant temperature thermal reservoir at 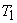 , does work , does work 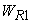 and rejects energy as heat and rejects energy as heat 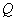 to the reservoir at to the reservoir at 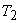 . The engine . The engine 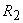 absorbs energy as heat absorbs energy as heat 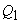 from the reservoir at from the reservoir at 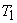 , does work , does work 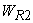 and rejects energy as heat and rejects energy as heat 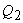 to the reservoir at to the reservoir at 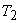 . Then . Then 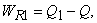 and and 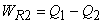
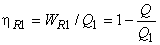 |
(19.4) |
and
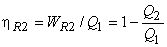 |
(19.5) |
By assumption, 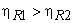
Then,
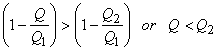 |
(19.6) |
Therefore, 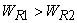
Since 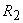 is a reversible engine, it can be made to execute the cycle in the reversed order. That is, when work is a reversible engine, it can be made to execute the cycle in the reversed order. That is, when work 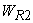 is performed on the device, it absorbs energy as heat, is performed on the device, it absorbs energy as heat, 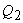 from the reservoir at from the reservoir at 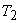 and rejects energy as heat and rejects energy as heat 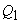 to the reservoir at to the reservoir at 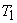 . Since, . Since, 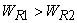 , , 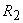 can be run as a heat pump utilizing part of the work done by can be run as a heat pump utilizing part of the work done by 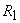 . The combination of the two devices is also shown in the figure. . The combination of the two devices is also shown in the figure.
The net work done by the device is given by
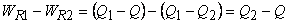 |
(19.7) |
- The resulting device absorbs energy as heat
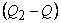 from the reservoir at from the reservoir at 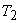 . .
- Does not require any interaction with the second reservoir.
- Delivers an equivalent amount of work.
This is in violation of the Kelvin-Planck statement of the second law of thermodynamics. Hence the assumption that 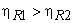 , is incorrect. Therefore, , is incorrect. Therefore,
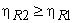 |
(19.8) |
Nov let us assume that the reversible engine 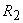 is more efficient then the reversible engine is more efficient then the reversible engine 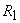 . Then the reversible engine . Then the reversible engine 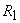 can be run as a heat pump, utilizing the part of the work done by can be run as a heat pump, utilizing the part of the work done by 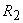 . By following the similar argument as the earlier case, we can arrive at the result that, . By following the similar argument as the earlier case, we can arrive at the result that,
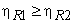 |
(19.9) |
Hence, it can be concluded that
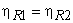 |
(19.10) |
Stated in works: All reversible engines operating between the two given thermal reservoirs have the same efficiency.
|