Equations (8.4) and (8.5) can be combined (eliminating t) to give
This equation suggests that the plot of 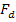 versus versus 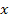 over a cycle generates an
ellipse, as shown in Fig. 8.2, with over a cycle generates an
ellipse, as shown in Fig. 8.2, with 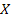 and and 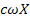 , respectively, as the semi-major
and minor axes. , respectively, as the semi-major
and minor axes.
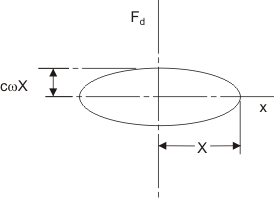
Figure 8.2: Damping force profile
The area of this ellipse signifies the energy dissipation per
cycle, which again, is
i.e., the same as given by eqn.(8.6).
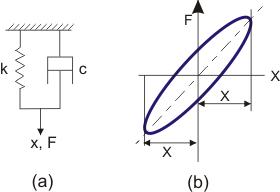
Figure 8.3: Energy dissipation

If the combined stiffness and damping of a vibrating system is modelled as
an ideal linear spring and a viscous dashpot in parallel (Fig. 8.4a), then, for
a harmonic displacement, the force displacement characteristic for every cycle
is obviously an elliptic loop as indicated in Fig. 8.3b.
This model, known as
the Kelvin-Voigt model, is commonly used to represent a real-life system.
Congratulations! You have finished module 2.
|