| |
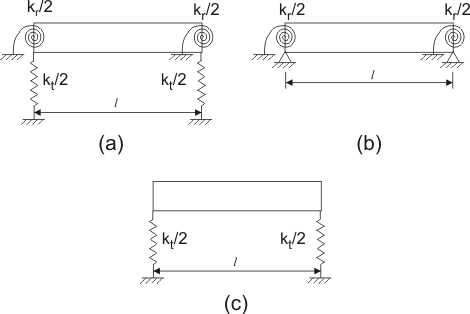
Figure 7.3: Stringer bending and torsion modes
- It has been shown that the lower ends
of the propagation bands are given by the natural frequencies of the element
shown in Fig.7.3b. The modes corresponding to these frequencies are called
the stringer torsion modes.
- The lower bounds of the propagation bands may be denoted by
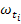 with with 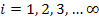
- The upper bounds of the propagation bands are
given by the natural frequencies of the flexural element shown in Fig. 7.3c. The modes
corresponding to these frequencies are called the stringer bending modes and denoted by
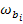 with with 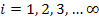
- Thus, the propagation
bands extend from
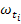 to to 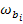 with with 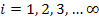 . It has been further shown
that, for an N-span periodic beam, a periodic element of which is shown
in Fig. 7.3a, every successive set of N natural frequencies is clustered within
each propagation band given by . It has been further shown
that, for an N-span periodic beam, a periodic element of which is shown
in Fig. 7.3a, every successive set of N natural frequencies is clustered within
each propagation band given by 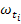 to to 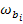 . So, for the natural frequencies to be widely separated, the values of . So, for the natural frequencies to be widely separated, the values of 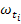 's should be minimum and those of 's should be minimum and those of 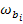 ' s maximum. In other words, the values of ' s maximum. In other words, the values of 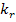 should
be low and those of should
be low and those of 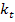 high, i.e., the stringer cross-section should be such that
it has a low torsional stiffness and a high bending stiffness. This automatically
suggests that the cross-section be open, such as Z-section and top-hat section. high, i.e., the stringer cross-section should be such that
it has a low torsional stiffness and a high bending stiffness. This automatically
suggests that the cross-section be open, such as Z-section and top-hat section.
Congratulations! You have finished Lecture 7.
|