The equation of motion can then be expressed as
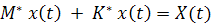 |
(40.8) |
Where,
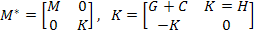 |
(40.8) |
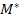 is a 2n dimensional positive definite matrix whereas is a 2n dimensional positive definite matrix whereas 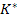 is neither positive definite nor symmetric. Considering the Cholesky decomposition of is neither positive definite nor symmetric. Considering the Cholesky decomposition of 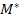 as as 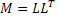 and introducing the transformation and introducing the transformation 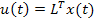 , the above state space equation can be written as , the above state space equation can be written as
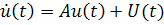 |
(40.9) |
Where, 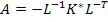 and and 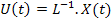 . The left and right eigenvalue problems associated with the transformed state equation are: . The left and right eigenvalue problems associated with the transformed state equation are:
In order to decouple the equations of motion, assuming the solution of Equation (40.9) of the form 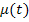 , where, , where, 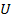 is the modal matrix, a model transformation can be carried out to get decoupled states as is the modal matrix, a model transformation can be carried out to get decoupled states as
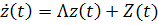 |
(40.10) |
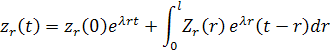 |
(40.11) |
Noting 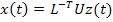 the above equation could also be written as the above equation could also be written as
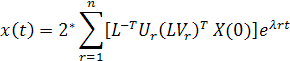 |
(40.12) |
Retaining only a finite numbers of frequencies, approximating the response of distributed parameter system the above equation can be expressed as:
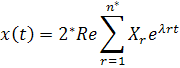 |
(40.9) |
Where, 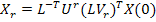 and and 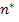 are the numbers of frequencies to be retained. The finite element routine and the described solutions scheme could be implemented in MATLAB environment taking advantage of the built in application routines for linear algebraic operations. are the numbers of frequencies to be retained. The finite element routine and the described solutions scheme could be implemented in MATLAB environment taking advantage of the built in application routines for linear algebraic operations.
Congratulations! You have finished the Course. |