Distributed Vibration Control of Symmetrically Laminated Composite Beam (Euler - Bernoulli Model)

At present, piezoelectric and magnetostrictive materials are the only smart materials, which are available in strip or patch form in the open market; hence these two materials are considered for numerical modelling. The use of magnetostrictive actuation is specially suited for one-dimensional structures such as robotic manipulator, or space antenna as it requires a coil enclosing the magnetostrictive layer to generate the required magnetic field. On the contrary, the piezoelectric elements are free from such constraints.

Most of the works in structural design of beams are carried out using classical beam theory or the Euler-Bernoulli model. Such a model is validated with the experimentally observed strain profile of a beam under combined stretching and bending. It is found, that for a large range of slenderness ratio (ratio of beam span to thickness) the model predicts fairly accurate variation of strain across the thickness of the beam. Hence, for the present discussion, in order to bring out the interaction mechanism of smart and host layer, the Euler-Bernoulli model is taken up.

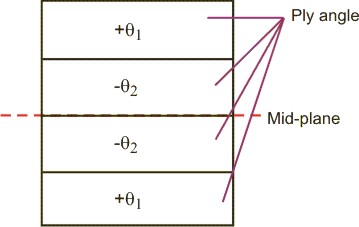
Figure 27.3: Symmetric laminated plane

Figure 27.3 shows a typical composite beam, where the ply angle are symmetric across the geometric mid-plane.

In order to develop a generalised model, the face beam is considered to be of composite material. The advantage of using composite as a host material is that the distributed layer need not be surface bonded but could be embedded inside the composite.

The modelling exercise is divided into two sections. In the first section, symmetrically laminated beams are considered. Here, the coupling between in plane and out of plane deformation is absent and hence the effect of smart layer addition on only the governing transverse equation of motion can be observed. In the next section, however, a more generalized case of unsymmetrical laminated beams are considered to discuss the coupling of in plane and out of plane motion.

Congratulations! You have finished Lecture 27.