Let us discuss the design of an observer when a system is in observer canonical form defined by the system matrices 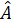 , , 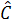 and and 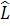 . In observer canonical form, these matrices are represented in the following way: . In observer canonical form, these matrices are represented in the following way:
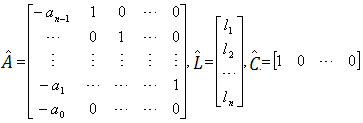 |
(26.5) |
Whenever, the desired eigen-values related to the error-dynamics are specified, one can construct the desired characteristic equation identical to eqn. (26.7). The observer gain matrix for such cases may be obtained from the simple relationship
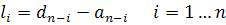 |
(26.6) |
Now, if a system is not in observer canonical form, then one needs to transform the system matrices first into canonical form. The transformation matrix required for such cases has been derived as
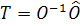 |
(26.7) |
where,  and and 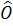 are the observability matrices related to the non-canonical and canonical forms respectively. After obtaining the observer gains in observer canonical form using eqn. (26.6), one can transform the gain vector to the original non-canonical form as are the observability matrices related to the non-canonical and canonical forms respectively. After obtaining the observer gains in observer canonical form using eqn. (26.6), one can transform the gain vector to the original non-canonical form as
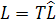 |
(26.8) |
Let us illustrate the process of estimator design with the help of an example.
|