The design of full-state feedback control presupposes the accessibility (possibility of sensing) of the complete state vector. For example, for figure 26.1, it is assumed that both the states, position and velocity are available for sensing. However, in reality, one may have only one of them available for direct sensing while the other state has to be estimated via simulation. Accepting that there will be finite error in this process, the focus is whether the error could be driven to zero at a faster rate than the plant-dynamics. Such a strategy is feasible only if the states are observable. The observability matrix of the system may be defined as

The states of a system could be estimated only if the rank of the matrix 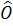is the same as size of the plant matrix A. After checking the observability of the system, one can go ahead with the design of the observer. Fig. 26.1 shows the block diagram representation of an observer based system.

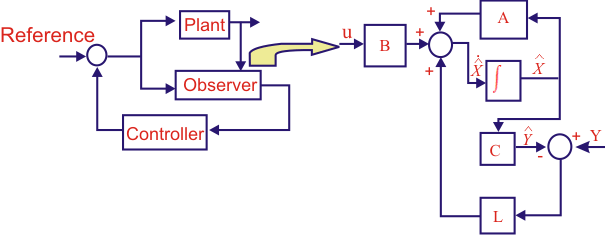
Figure 26.1: Observer based system