Example
A SDOF system has the following mass, stiffness and damping constant in appropriate units,
m =0.1, c =0.001 and k =0.5;
Design a full-state feedback control, with an actuator influence matrix BT = [0 1] and a forcing function 0.1u(t) (u(t) – unit step function), such that the desired eigen-values are at -1± 1j, respectively.
Solution
The equation of motion of the system may be written as
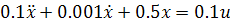 |
|
or, 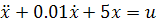 |
The equation of motion can be represented in state-space form by constructing the state vector as
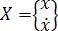 , ,
Accordingly,
We first check the controllability of the matrix; the controllability matrix may be computed using eqn. (29.12) as
Since the rank of the controllability matrix is 2, the same as the size of A, hence the system is controllable. Next, we find the characteristic equation of the open loop system by finding the eigen- values of the system as: [-0.0050 + 2.2361j, -0.0050 - 2.2361j];
The desired characteristic equation is given by
Since the system is already in control-canonical form, the gain matrix KC is
Congratulations! You have finished Lecture 25. |