The frequency-dependence of the complex modulus we have just discussed
can be explained through a linear viscoelastic model. For example, consider the
simple, three-element model shown in the figure below:
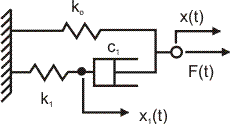
Figure 14.2: 3 Element model
The stress-strain relation
for this model is given by the following equation
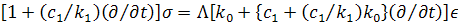 |
(14.1) |
where 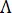 is a geometric parameter. is a geometric parameter.
Assuming a harmonic loading of frequency 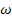 ,
we substitute ( ,
we substitute (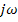 ) for the operator ) for the operator 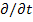 in this equation. Then, we get the
complex modulus as in this equation. Then, we get the
complex modulus as
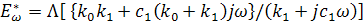 |
(14.2) |
Taking the real and imaginary parts of this equation, we obtain
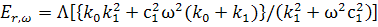 |
(14.3) |
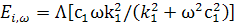 |
It can be seen from eqns. (14.3) that the loss modulus 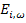 has a maxima
at has a maxima
at 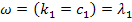 , where , where 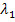 is the relaxation parameter of the viscous branch. is the relaxation parameter of the viscous branch.
Congratulations! You have finished Lecture 14.
|