Module 3: Dynamic Properties and Selection of Materials
Lecture 10: Selection Criteria for Linear Hysteretic Materials
Let us now illustrate through an example
how the results in the table can be used to select a structural material.
Example: A beam of specific mass and rectangular cross-section (width "b" and thickness "h") has to
be designed. The length and width of the beam are specified but its height is left as
a variable. Determine the figure of merit (FOM) for selecting the beam material
so that the maximum displacement amplitude is minimum under a harmonic loading.
Solution
For the maximum displacement amplitude to be minimum, the quantity should be maximum.
In this problem, should be maximum for the material to be chosen. With a
given width, for bending vibration, the stiffness , where is the
height of the beam and is Young's modulus.
Now, for a specified mass and
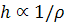
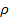
with h as the only variable, , whereis the density.
So, .
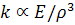
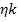
Hence, for to be maximum, the quantity should be maximum.
Thus, the best material is the one for which the quantity is maximum. This quantity (a function of only the material properties) to be
maximized is called the FOM against damping.
Consider the following structural materials
Material
Mod of Elasticity (GPa)
Loss factor
Density
FOM
Steel
200
0 (10-3)
7500
= 4.74 × 10−4
Brass
105
0 (10-4)
8500
= 1.71 × 10−5
Aluminium
70
0 (10-5)
2700
= 3.18 × 10−5
The table suggests steel to be the best structural material against minimisation of maximum displacement and aluminium to be the next best material even though brass has higher loss factor than aluminium.
should be maximum.
should be maximum for the material to be chosen. With a
given width, for bending vibration, the stiffness 
, where 
is the
height of the beam and 
is Young's modulus. 
, where 
is the density. 
.
Hence, for 
should be maximum.
