Analysis of Scatter
We now return to the question of determining the uncertainty in a variable arising from scatter. Let 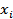 , , 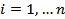 be be 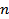 different readings of the variable different readings of the variable 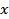 obtained from obtained from 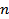 distinct but nominally identical (similar) experiments. The mean distinct but nominally identical (similar) experiments. The mean 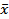 and variance and variance 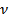 for the set for the set 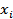 are formally defined as are formally defined as
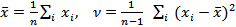
and the standard deviation 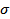 is equal to is equal to 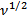 . The quantity . The quantity 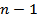 in the definition of in the definition of 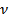 arises from the loss of one degree of freedom in forming the sum due to the presence of arises from the loss of one degree of freedom in forming the sum due to the presence of 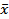 . If . If 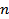 is large, the probability distribution function is large, the probability distribution function 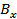 of the variable of the variable 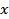 can be assumed to be Gaussian in view of the central limit theorem (refer Probability Density Function Approach of Lecture 3). Hence, the scatter of values can be assumed to be Gaussian in view of the central limit theorem (refer Probability Density Function Approach of Lecture 3). Hence, the scatter of values 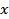 about the mean about the mean 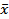 follows the formula follows the formula
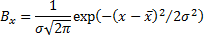
|