Example: Given 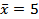 and and 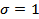 find the probability that the value of find the probability that the value of 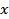 in a new experiment is (1) between 4.5 and 5.5, (2) between 4.5 and 5.75, (3) less than 6.5 and (4) between 6 and 7. in a new experiment is (1) between 4.5 and 5.5, (2) between 4.5 and 5.75, (3) less than 6.5 and (4) between 6 and 7.
Let 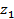 and and 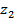 be the limits between which the probability must be determined. The values of be the limits between which the probability must be determined. The values of 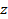 in each case are (1) in each case are (1) 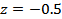 and 0.5, (2) and 0.5, (2) 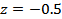 and 0.75, (3) and 0.75, (3) 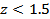 and (4) and (4) 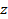 between 1 and 2. The required probabilities are between 1 and 2. The required probabilities are 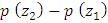 ; hence in (1), this quantity is ; hence in (1), this quantity is 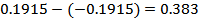 ; in (2), ; in (2), 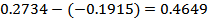 ; in (3), ; in (3), 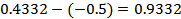 and in (4), and in (4), 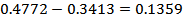 . .
The most commonly used probability interval called the 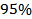 confidence interval corresponds to confidence interval corresponds to 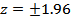 since since 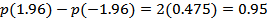 . Hence normally distributed scatter can be specified as . Hence normally distributed scatter can be specified as 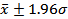 with with 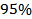 confidence. For convenience this interval is written as confidence. For convenience this interval is written as 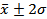 . Gaussian distribution for scatter can be assumed if the number of repetitive experiments is greater than 30. . Gaussian distribution for scatter can be assumed if the number of repetitive experiments is greater than 30.
For 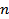 points with a mean points with a mean 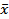 , points that fall outside a probability value of , points that fall outside a probability value of 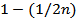 are to be rejected. The mean and the variance are to be rejected. The mean and the variance 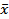 and and 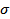 must then be recalculated. This is called Chauvenet's criterion for statistical rejection of data. The criterion can be applied only once to the data set. It determines the acceptable level of scatter in an experiment arising from a large number of random influences. must then be recalculated. This is called Chauvenet's criterion for statistical rejection of data. The criterion can be applied only once to the data set. It determines the acceptable level of scatter in an experiment arising from a large number of random influences.
|