| |
Remarks
- Beer's law (Equation 7.1) can be applied to solid, liquid and gaseous media.
- Equation 7.1 is equivalent to stating that
- In other words, the reduction in radiation intensity is proportional to the intensity at that location and the thickness over which the change is being determined.
- The process of absorption shows that the equivalent transmittivity decreases with increasing
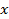 , Equation 7.2, and hence the thickness of the material. For transmittivities much less than unity , Equation 7.2, and hence the thickness of the material. For transmittivities much less than unity 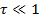 , the layer is said to be optically thick . When , the layer is said to be optically thick . When 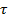 is close to unity, the layer is said to be optically thin . is close to unity, the layer is said to be optically thin .
- A material layer can be optically thick at one wavelength but optically thin at another. For an example, see Figure 7.3.
- When a material is optically thick, all the radiation leaving a surface is fully absorbed in a region of small thickness.
- The absorption coefficient
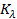 depends on the nature of scattering elements in the gas, chemical composition and concentration of species. In addition, it can depend on pressure and temperature. Beer's law brings out the dependence of light attenuation on distance, but all other contributing factors are lumped into the absorption coefficient. depends on the nature of scattering elements in the gas, chemical composition and concentration of species. In addition, it can depend on pressure and temperature. Beer's law brings out the dependence of light attenuation on distance, but all other contributing factors are lumped into the absorption coefficient.
- Extensive tabulation of absorption coefficient is available in the literature.
- In semi-transparent media, the material will exhibit refraction effects ( namely, changes in the speed of propagation of light ) as well as absorption ( attenuation in the energy transmitted ). Refractive index jointly with absorption coefficient is then viewed as the real and imaginary parts of a complex property ( complex refractive index ) of wave propagation. The composite property, as expected, scales with material density. While this interpretation of a complex property is required in radiation analysis of energy transfer, it has not been exploited in measurements and is not discussed here.
|
| |
| |
| |
| |
| |
| |
| |
| |
| |
| |
| |
| |
| |
| |
|
|
|
|