The Buckingham- 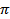 theorem is useful in this context. The dimensionless form of the drag equation can be easily derived as theorem is useful in this context. The dimensionless form of the drag equation can be easily derived as
where 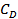 is the drag coefficient, and Re is Reynolds number based on the velocity is the drag coefficient, and Re is Reynolds number based on the velocity 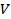 and dimension and dimension 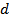 . The statements of principles of similarity can now be stated as . The statements of principles of similarity can now be stated as

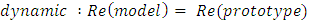
If conditions of similarity are satisfied, the dimensionless drag coefficient recorded in experiments will be equal to one for the prototype at every Reynolds number.
The dimensionless expression in terms of the drag coefficient shows the following: If fluid properties in the laboratory and field experiments are identical, the similarity principle requires the respective Reynolds numbers to be equal. Equivalently, we require the product 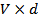 for the model and the prototype to be equal, as stated in the numerical example above. for the model and the prototype to be equal, as stated in the numerical example above.
|