The temperature recorded by the liquid crystal sheet can be equated to the temperature of the thin aluminum plate mounted on the surface of the upper bakelite sheet. Owing to its high thermal conductivity and small thickness, the temperature drop through the aluminum sheet can be taken to be negligible. This temperature, as a function of space and time will then prevail over the bakelite sheet as well. The Bakelite sheet serves as a semi-infinite solid with experimentally determined wall temperature boundary conditions.
For a semi-infinite solid, the 1-D transient heat conduction equation is given as
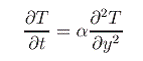
The related wall boundary condition is
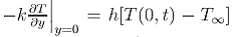
The analytical solution of the diffusion equation is
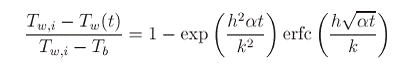
Here, Tw(t) is the surface temperature at time t, Tb is the bulk temperature inside the channel, Tw,i is the initial surface temperature, h is the convective heat transfer coefficient, α is the thermal diffusivity and k is the thermal conductivity of the Bakelite plate. The local bulk temperature can be determined by interpolating the temperatures at the inlet and the exit of the test section.
The transient non-dimensional temperature variation of the test surface can be curve-fitted by using the least square approximation where the local heat transfer coefficient h is a parameter. Parameter estimation falls in the general class of inverse techniques and the above formulation classifies as an inverse transient method.
|