| |
Figure 5.19 and Figure 5.20 show the transient evolution of the convective field for experiments when the growing crystal is respectively held stationary in the solution and rotated at a constant speed of 15 rpm. The ramp rate to cool the solution in the two sets of experiments is 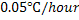 . Insertion of the seed into its supersaturated solution can lead to an instantaneous temperature difference between them, followed by an initial dissolution of the crystal. This phase of the experiment is not included in the figures. With the passage of time, thermal equilibrium is established, and density differences within the solution are solely due to concentration differences. Adjacent to the crystal, the deposition of solute from the solution to the crystal surfaces results in a change of concentration and the solution goes from supersaturated to the saturated state. In the absence of rotation, the denser solution displaces lighter solution in the vicinity of the crystal and a circulation pattern is set up around the crystal. The fluid motion is largely in the vertical plane. With rotation, a radial pressure gradient creates an independent circulation loop that forms an alternative basis of solute movement. Here, the fluid particles around the crystal move in the radial direction, but conservation of mass ensures that vertical velocities be set-up once again. In the purely buoyancy-driven mode (0 rpm; also called natural convection), the strength and orientation of the convection currents is determined by the available concentration difference in the solution at any instant of time, and hence the cooling rate. On the other hand, an externally imparted rotation to the growing crystal (called forced convection) leads to homogenization of the solution, reduction in concentration gradients and hence a reduction in the strength of convection currents. Except for the initial stages of the growth process (where it is diffusion-dominated), these circulation patterns and their interaction form the basis of the transport of solute from the bulk of the solution to the growing crystal surfaces. . Insertion of the seed into its supersaturated solution can lead to an instantaneous temperature difference between them, followed by an initial dissolution of the crystal. This phase of the experiment is not included in the figures. With the passage of time, thermal equilibrium is established, and density differences within the solution are solely due to concentration differences. Adjacent to the crystal, the deposition of solute from the solution to the crystal surfaces results in a change of concentration and the solution goes from supersaturated to the saturated state. In the absence of rotation, the denser solution displaces lighter solution in the vicinity of the crystal and a circulation pattern is set up around the crystal. The fluid motion is largely in the vertical plane. With rotation, a radial pressure gradient creates an independent circulation loop that forms an alternative basis of solute movement. Here, the fluid particles around the crystal move in the radial direction, but conservation of mass ensures that vertical velocities be set-up once again. In the purely buoyancy-driven mode (0 rpm; also called natural convection), the strength and orientation of the convection currents is determined by the available concentration difference in the solution at any instant of time, and hence the cooling rate. On the other hand, an externally imparted rotation to the growing crystal (called forced convection) leads to homogenization of the solution, reduction in concentration gradients and hence a reduction in the strength of convection currents. Except for the initial stages of the growth process (where it is diffusion-dominated), these circulation patterns and their interaction form the basis of the transport of solute from the bulk of the solution to the growing crystal surfaces.
Figure 5.19 shows the sequence of convection patterns in the purely buoyancy-driven mode. Growth in the initial stages of the experiments is accompanied by steady, weak convection, during which diffusion effects can be expected to be significant. Thus, for t = 20 hours, a slow growth of the crystal is to be expected. Concentration gradients are primarily localized in the vicinity of the growing crystal. With the passage of time, the size of the crystal increases, and the gradients grow in strength. This result is brought out in the schlieren images as an increase in the light intensity around the crystal. As defined by the bright region, the resulting flow creates a strong plume directly above the growing crystal. Over a longer period of time (20-90 hours), the plume structure remains unchanged. It indicates a stable growth regime for the crystal, where the buoyant plumes are steady and uniform in nature (Figure 5.19(v-vii)). A gradual evolution of the concentration gradients and the associated buoyant plumes ensure a relatively uniform concentration field in the vicinity of the growing crystal, thus leading to symmetric growth of the crystal at the greatest possible rate. As the crystal increases in size, the convection currents grow in strength. Beyond 90 hours, they are seen to become quite vigorous (Figure 5.19(viii)). Correspondingly, time-dependent movement of the plumes was seen in the experiments. This stage is characterized by local changes in the concentration gradients in the vicinity of the growing crystal, followed by a breakdown in the symmetry of the growth process. It is a limit on the time duration up to which a single growth experiment can be carried out in free convection regime, and the consequent limit on the size of the grown crystal.
|