For correlated signals 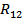 has information regarding the phase difference between has information regarding the phase difference between 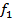 and and 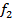 . For example, if . For example, if 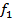 and and 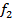 are harmonic with phase difference are harmonic with phase difference 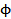 , , 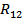 is also harmonic with a starting value that depends on is also harmonic with a starting value that depends on 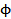 . It is thus a convenient measure of the phase difference itself. If . It is thus a convenient measure of the phase difference itself. If 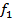 and and 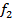 are random signals are random signals 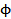 will be a function of the frequency variable will be a function of the frequency variable 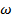 . In such problems we work with the cross-spectral function . In such problems we work with the cross-spectral function 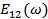 defined as defined as
In wave propagation problems, 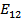 has information regarding has information regarding 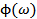 and hence the wave number distribution and the wave speeds as a function of frequency. In nonlinear dynamics this is further interpreted in terms of appearance of coherent structures. and hence the wave number distribution and the wave speeds as a function of frequency. In nonlinear dynamics this is further interpreted in terms of appearance of coherent structures.
The following results can be easily derived.
If 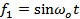 and and 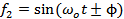 , , 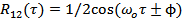 and and 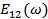 is a delta function centred at is a delta function centred at 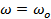 . One can calculate . One can calculate 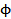 from from 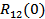 . In a travelling wave problem, . In a travelling wave problem, 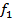 and and 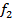 may be two signals obtained from probes separated by a distance may be two signals obtained from probes separated by a distance 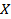 . The wave number is then given as . The wave number is then given as 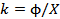 . If . If 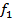 is white noise and is white noise and 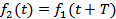 , i.e. , i.e. 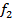 is a time shifted form of is a time shifted form of 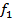 , one can show that , one can show that 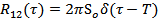 where where 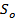 is the power spectrum of is the power spectrum of 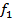 (and a constant if (and a constant if 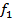 is white noise). Subsequently it is easy to show that is white noise). Subsequently it is easy to show that 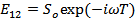 and and 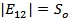 . .
|