Fourier Transform Technique
The complex function 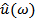 is defined as the Fourier transform of is defined as the Fourier transform of 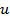 and is calculated as and is calculated as
The normalized power spectrum can then be calculated as
where 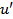 is the RMS value of is the RMS value of 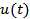 . It is possible to show that . It is possible to show that 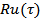 and and 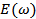 from a Fourier transform pair, i.e. from a Fourier transform pair, i.e.
Methods of calculating Fourier transforms are well-established. In particular, the fast Fourier transform (FFT) algorithm has found wide usage both in software and in hardware applications in signal processing. Hence it is to be understood that integrals appearing in the Fourier transforms defined above can be readily determined.
Though the integrals given above are complex-valued, the property 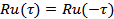 guarantees that guarantees that 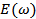 is purely real. On the other hand, the Fourier integral for is purely real. On the other hand, the Fourier integral for 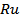 is to be interpreted as the real part of the complex function. Typical autocorrelation functions and power spectrum are sketched in Figure 1.10. is to be interpreted as the real part of the complex function. Typical autocorrelation functions and power spectrum are sketched in Figure 1.10.
|