|
Classification of data
Data received by an observer from an experimental setup can be classified as in Figure 1.7. Methods of analyzing deterministic data are well-established because the data is already in a form, from which integral measures can be extracted. When periodic signals are encountered it is a conventional practice to present results for sinusoidal signals alone. This is because results for a general periodic signal can be constructed from those for harmonic signals using Fourier decomposition of the form
Here 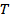 is the time period of the signal is the time period of the signal 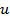 and the Fourier coefficients and the Fourier coefficients 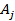 satisfy the condition satisfy the condition 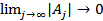 , The coefficients can be determined from the formula , The coefficients can be determined from the formula
As an example, pressure drop in a pipe carrying pulsatile flow can be determined as a weighted average of the individual pressure drops occurring in sinusoidally varying flows whose frequencies are integer multiples of that of the real problem.
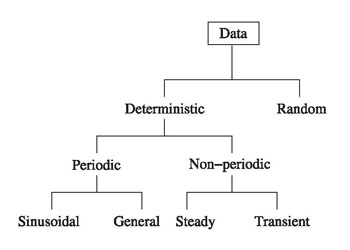
Figure 1.7: Classification of Data |
When the data available to the observer is random, one is forced to use statistical techniques. This is because even when a mean value is determinable, one requires prior knowledge of the length of the signal to be considered for averaging. This mean value can subsequently be used for deterministic analysis. However in many applications information the randomness itself may be desired and statistical measures of the signal will have to be calculated.
|