Numerical Solution of the Poisson Equation

The governing equation of the shadowgraph process (Equation 44) relates the intensity variation in the shadowgraph image to the refractive index field of the inhomogeneous medium. In order to solve the equation to obtain the refractive index, the following numerical procedure is adopted. First, the Poisson equation is discretized over the physical domain of interest by a finite-difference method. The resulting system of algebraic equations is solved for the image under consideration to yield a depth averaged refractive index value for each node point of the grid. A mix of Dirichlet and Neumann boundary conditions are used for the purpose. The refractive index conditions typically used on the boundaries of a crystal growth chamber are shown inn Figure 5.9. A computer code can be written for solving the Poisson equation, and it can be validated against analytical examples.

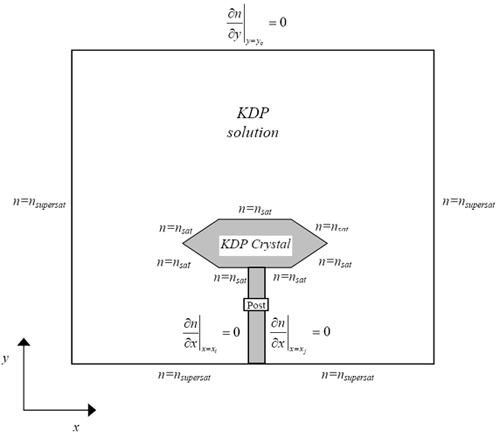
Figure 5.9: Refractive index specification on the boundaries.

The experimental input to the code is in the form of a matrix containing the gray value of each pixel of the shadowgraph image. The output generated by the Poisson solver is a matrix containing the averaged refractive index at each node point of the grid. Since the relationship between thee refractive index and the concentration of the KDP saturated solution at different temperatures is well documented, the refractive indices can be related to concentration over every frame of the image record.