Assumption 2 : The assumption of the infinitesimal displacement inside the growth chamber can be extended and taken to be valid even for the region falling between the screen and the exit plane of the chamber. As a result, the coordinates of the ray on the screen can be written as
The deviation of the rays from their original paths in occurs through the inhomogeneous medium. In the absence of the inhomogeneous field, such an area is a regular quadrilateral. It transforms to a deformed quadrilateral when imaged on to a screen in the presence of the inhomogeneous field. The summation in the above equation extends over all the rays passing through points 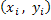 at the entry of the test section that are mapped onto the small quadrilateral at the entry of the test section that are mapped onto the small quadrilateral 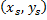 on the screen. Considering the fact that the area of the initial spread of the light beam gets deformed on passing through the refractive medium, the intensity at point on the screen. Considering the fact that the area of the initial spread of the light beam gets deformed on passing through the refractive medium, the intensity at point 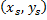 is is
where 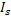 is the intensity on the screen in the presence of the inhomogeneous refractive index field, and is the intensity on the screen in the presence of the inhomogeneous refractive index field, and 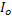 is the original undisturbed intensity distribution. The denominator in the above equation is the Jacobian is the original undisturbed intensity distribution. The denominator in the above equation is the Jacobian 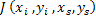 of the mapping function of of the mapping function of 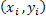 onto onto 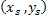 as shown in Figure 5.8. as shown in Figure 5.8.
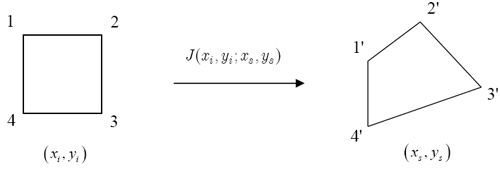
Figure 5.8: Jacobian 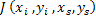 of the mapping function of the mapping function 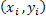 onto onto 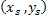
Geometrically it represents the ratio of the area enclosed by four adjacent rays after and before passing through the inhomogeneous medium. In the absence of the inhomogeneous field, such an area is a regular quadrilateral. It transforms to a deformed quadrilateral when imaged on to a screen in the presence of the inhomogeneous field. The summation in the above equation extends over all the rays passing through points 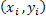 at the entry of the test section that are mapped onto the small quadrilateral at the entry of the test section that are mapped onto the small quadrilateral 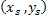 on the screen and contribute to the light intensity within. on the screen and contribute to the light intensity within.
|