Testing of Tomographic Algorithms

The ART, MART and the optimization algorithms have been for variety  of cases by subbarao et al. [32]. In the examples, the temperature fields were synthetically generated. Hence it was possible to determine explicitly the convergence properties and errors for each of the methods. Among the various algorithms, the authors have identiflied MART3 as the best in terms of the error and CPU time requirements. The AVMART algorithms proposed by the author and his coworkers have been validated in the present section against two benchmark cases (1) a circular region with five holes, and (2) the numerically generated three-dimensional temperature field in fluid convection. Employing a temperature field similar to that encountered in the experiments aids in the choice of the proper initial guess and error levels to be anticipated. This also helps in selecting the proper tomographic algorithm. The algorithms stated in Sections MART and AVMART have been rested for a circular region with distribution of holes and a numerically generated three-dimensional temperature field in Rayleigh-Benard convection. Sensitivity of the algorithms to noise has been tested in the context of numerically generated temperature data. Issues addressed in the sensitivity study are initial guess, noise in projection data, and the effect of increasing number of projections on the accuracy of reconstruction.

Reconstruction of a Circular Disk with Holes

A circular region with five symmetrically placed holes is considered. The object is recognized in terms of the local dimensionless density, which is zero at the holes and unity elsewhere. To implement the reconstruction algorithm, it is convenient to enclose the circular object within a square domain. The gap between the circle and the square is specified to have zero density (in calculations, a value of 0.001 has been used for zero density). The square region is discredited into 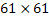cells in the x and y directions. Projections of this object have been determined analytically and hence exact. The recovery of the original object from a limited number of these projections using the original MART as well as the proposed AVMART algorithms is discussed below.

Projections at angles of 0, 45, 90,and 135 degrees have been considered in the present application. The initial guess for the density field was a constant value of unity. A convergence criterion of 1% for the iterations has been uniformly used. At a Convergence of 0.01% , the solution was practically identical, except that errors were seen to be marginally higher. This feature of topographic algorithms, that convergence is asymptotic (but not monotonic) has been reported earlier. Such trends are to be expected in the reconstruction of fields having a step discontinuity. At the hole boundary in the present example. The relaxation factor was set at 0.1in case of original MART while it was unity in the AVMART algorithms. All calculations were carried out on a DEC–alpha workstation with 196 MB RAM and a 223 MHz processor.

A summary of the reconstructed fields using the three original and three proposed algorithms is shown in Fields 33. In principle, all the six algorithms were seen to converge to a qualitatively meaningful solution. The void fraction, namely the fraction of the space occupied by the holes was 0.34 in the present application. In the reconstructed solution, the void fraction can be determined from the formula

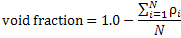
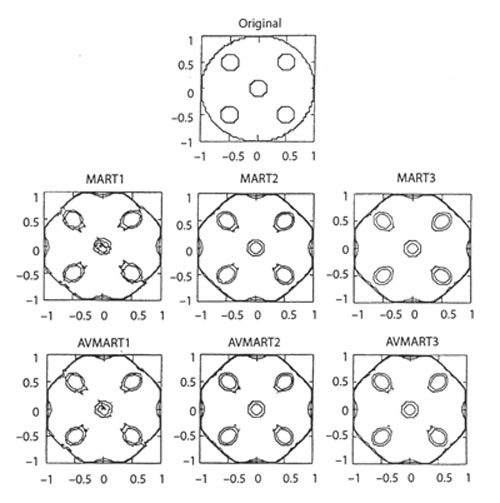
Figure 4.65: Original and Reconstructed density fields of a circular region with holes (the outer circle appears as an octago because of a finite number of view angles employed).