Iterative Techniques
Series expansion methods are perhaps the most appropriate tomographic technique for interferometry since they work limited projection data. These methods are iterative in nature and consist necessarily of four major steps, namely:
- initial assumption of the field to be reconstructed over a grid,
- calculation of the correction for each pixel,
- application of the correction, and
- test for convergence,
The central idea behind the calculation of the correction (step2) is the following.
With the assumed field, one can explicitly compute projection values by numerical integration. The difference between the computed projection and experimentally recorded projection data is a measure of the error in the assumed solution this error can be redistributed to the pixels so that error is reduced to zero. Repetition of these steps is expected to converge to a meaningful solution. The series expansion techniques differ only in the manner in which the errors are redistributed over the grid.
The word convergence in step 4 is used in an engineering sense as a stopping criterion for the iterations, and not in the strict mathematical sense, where a formal proof is needed to show convergence of the numerical solution to the exact solution
The iterative methods require the discretization of the plane to be reconstructed by a rectangular grid (Figure 4.66). The length of the intercept of the i-th ray with the j–th cell in given projection is known as the weight function wij. It can be shown that
where 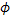 refers to the projection data. The number of unknowns N in most cases is much larger than the number of unknowns M. This discretization produces a matrix equation refers to the projection data. The number of unknowns N in most cases is much larger than the number of unknowns M. This discretization produces a matrix equation
The problem of reconstruction thus is a problem of inversion of a rectangular matrix. Iterative techniques that are used in the tomography can be viewed as developing a generalized inverse of the matrix 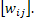 This matrix in a typical laser tomography problem has large dimensions for the differentially heated fluid layer, the greatest matrix size encountered was This matrix in a typical laser tomography problem has large dimensions for the differentially heated fluid layer, the greatest matrix size encountered was 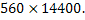 This is a sparse matrix with many of its elements being zero. General purpose matrix libraries cannot be used to invert such matrices since they are highly ill-conditioned and rectangular in structure. The tomographic algorithms can be seen as a systematic route towards a meaningful inversion of the matrix equation. This is a sparse matrix with many of its elements being zero. General purpose matrix libraries cannot be used to invert such matrices since they are highly ill-conditioned and rectangular in structure. The tomographic algorithms can be seen as a systematic route towards a meaningful inversion of the matrix equation.
|