Strouhal Number

Table 2 compares the Strouhal number from the present work with that of other investigations at similar Reynolds numbers and zero degree orientation. A maximum deviation of 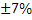between the present work and that of other investigations is indicated in Table 2. The difference between the present study and literature can be attributed to the difference in aspect ratio, blockage and inlet turbulence level. Figure 3.45 shows the comparison of the present experiments with the published literature in terms of Strouhal number for a circular cylinder (top) and square cylinder (bottom). Various Reynolds numbers have been considered. Each individual data set shows only a weak dependence of Strouhal number on Reynolds number. A certain level of scatter is visible. Data recorded in the present experiments at aspect ratios 16, 28 and 60 are shown by shaded and unshaded diamonds and unshaded squares. Broadly, these three lines bound the Strouhal number values reported in the literature. Thus, one can conclude that aspect ratio can explain the minor discrepancy in Strouhal number data of a square cylinder. The experimental data of the present study in Figure 3.45 show that Strouhal number increases with an increase in aspect ratio. The trend recorded for a circular cylinder by Norberg (1994) is supported by the present study.

Table 2: Comparison of Strouhal number with the published literature for flow past a square cylinder.