Data Analysis from Velocity Vectors
In applications, the velocity information is often necessary but not sufficient and other
quantities will be of interest as well. The velocity field obtained from PIV measurements
can be used to estimate relevant quantities by means of differentiation and integration.
The vorticity field is of special interest because, unlike the velocity field it is independent
of the frame of reference. In particular, if it is resolved temporally, the vorticity field
can be much more useful in the study of flow phenomena than the velocity field. This
is particularly true in highly vortical flow such as turbulent shear layers, wake vortices
and complex vortical flows. Integral quantities can also be obtained from the velocity
data. The instantaneous velocity field obtained by PIV can be integrated, yielding either
a single path integrated value or another field such as the stream function. Analogous
to the vorticity field, the circulation obtained through path integration is also of special
interest in the study of vortex dynamics, mainly because it is also independent of the
reference frame. In the following section, data analysis for calculation of various derived
quantities from PIV measurements are presented.
Velocity differentials
The differential terms are estimated from the velocity vectors obtained from PIV. Since
PIV provides the velocity vector field sampled on a two dimensional evenly spaced grid
specified as 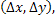 finite differencing can be employed to get the spatial derivatives.
There are a number of finite difference schemes that can be used to obtain the derivatives.
The truncation error associated with each operator is estimated by means of a
Taylor series expansion. The actual uncertainty in differentiation is due to that in the
uncertainty of the velocity estimate finite differencing can be employed to get the spatial derivatives.
There are a number of finite difference schemes that can be used to obtain the derivatives.
The truncation error associated with each operator is estimated by means of a
Taylor series expansion. The actual uncertainty in differentiation is due to that in the
uncertainty of the velocity estimate 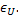 It can be obtained using standard error propagation
methods assuming individual data to be independent of the other. There are two
schemes that reduce the error associated with differentiation: Richardson extrapolation
and least squares approach. The former minimizes the truncation error while the least
squares approach reduces the effect of random error, i.e. the measurement uncertainty, It can be obtained using standard error propagation
methods assuming individual data to be independent of the other. There are two
schemes that reduce the error associated with differentiation: Richardson extrapolation
and least squares approach. The former minimizes the truncation error while the least
squares approach reduces the effect of random error, i.e. the measurement uncertainty, 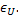 These approaches are briefly discussed bellow. These approaches are briefly discussed bellow.
Least squares estimate of the first derivative:
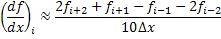
Here, the accuracy is of the order of 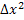 and the associated uncertainty is and the associated uncertainty is 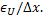
The derivative using Richardson extrapolation is calculated as:
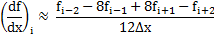
The accuracy of the above approximation is of order 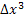 and the uncertainty associated
with the expression is and the uncertainty associated
with the expression is 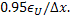
|