| |
The 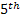 and and 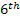 terms in the turbulent kinetic energy equation are termed as
viscous diffusion and pressure diffusion respectively. The sum of these two terms has
been obtained as the residual of the turbulent kinetic energy equation. It should be
noted that the viscous diffusion can be expected to be insignificant at intermediate and
high Reynolds number. Therefore the residual term is primarily due to the pressure
transport. terms in the turbulent kinetic energy equation are termed as
viscous diffusion and pressure diffusion respectively. The sum of these two terms has
been obtained as the residual of the turbulent kinetic energy equation. It should be
noted that the viscous diffusion can be expected to be insignificant at intermediate and
high Reynolds number. Therefore the residual term is primarily due to the pressure
transport.
The individual budget terms of the turbulent kinetic energy equation can be
calculated from PIV measurements. It may be assumed that the total kinetic energy is
1.33 times that of that measured from two dimensions. Panigrahi et al., (2005) have validated
the above assumptions from an experiment on flow past a rib using 2-component
and stereo-PIV.
The dissipation term of the kinetic energy budget equation has been calculated
based on the assumption of both local isotropy and axisymmetry. The assumption of local
isotropy requires the eight ratios of velocity
fluctuations to be equal to unity. Schenck and
Jovanovic (2002) reported the eight isotropic ratios to be in the range of 0.4 to 1.7 from
hotwire measurements of the plane wake of a circular cylinder and axisymmetric wake
of a sphere. The diffusion term in the turbulent kinetic energy equation is calculated
using the assumptions: 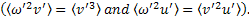 The above assumption
has also been justified by Panigrahi et al. (2005) through experiments involving flow
past a rib. The above assumption
has also been justified by Panigrahi et al. (2005) through experiments involving flow
past a rib.
|