| |
Lumped Analysis
A lumped parameter analysis of probes is given below. The effect of spatial variability is discussed through specific examples later in this chapter. Let 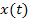 be the flow input and be the flow input and 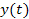 the probe output. The order of a probe, a transducer or a measurement system is determined by the order of the differential equation relating the probe output. The order of a probe, a transducer or a measurement system is determined by the order of the differential equation relating 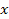 and and 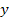 with time with time 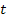 as the independent variable. Hence we have: as the independent variable. Hence we have:
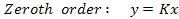
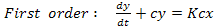
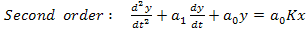
In the above equations 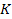 is the static sensitivity of the probe that can be determined once-and-for-all from a steady state experiment. Consider the response of these systems to a step input is the static sensitivity of the probe that can be determined once-and-for-all from a steady state experiment. Consider the response of these systems to a step input 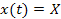 , a constant and a periodic input , a constant and a periodic input 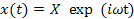 . Here . Here 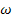 is frequency and is frequency and 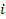 the imaginary unit the imaginary unit 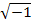 . For a step input, we assume the initial conditions to be quiescent, i.e., . For a step input, we assume the initial conditions to be quiescent, i.e., 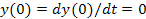 . For a periodic input we assume that the system has reached a dynamic steady state and the output . For a periodic input we assume that the system has reached a dynamic steady state and the output 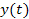 oscillates with the same frequency as the forcing frequency oscillates with the same frequency as the forcing frequency 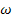 . The second part of this assumption is strictly true only for linear systems, i.e. coefficients . The second part of this assumption is strictly true only for linear systems, i.e. coefficients 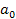 , , 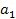 , , 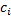 and and 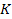 are independent of are independent of 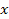 , , 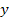 and and 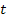 . In both laboratory and field experiments the fluctuations in the input will displace the measurement system only marginally with respect to the operating point and so its performance can be locally linearized. Hence the linear analysis presented here is not severely restrictive. . In both laboratory and field experiments the fluctuations in the input will displace the measurement system only marginally with respect to the operating point and so its performance can be locally linearized. Hence the linear analysis presented here is not severely restrictive.
|