Applying Taylor's series approximation for a small change in the value of 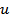
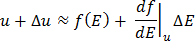
where the series has been truncated after the first term. Setting 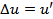 and and 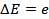 , we get , we get
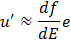
Here, the quantity 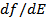 is the gradient of the calibration curve evaluated at the operating point is the gradient of the calibration curve evaluated at the operating point 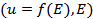 . The error due to truncating the Taylor series is usually small if . The error due to truncating the Taylor series is usually small if 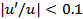 . The truncation error in calculating . The truncation error in calculating 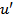 can be reduced by working with an extended Taylor's series expansion can be reduced by working with an extended Taylor's series expansion
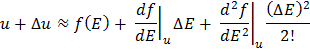
wherein the higher order term 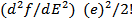 has been included. This approach is useful provided the higher order derivative can be determined accurately. In practice, the calibration curve is experimentally constructed and these higher order derivatives can be computed only with substantial error. has been included. This approach is useful provided the higher order derivative can be determined accurately. In practice, the calibration curve is experimentally constructed and these higher order derivatives can be computed only with substantial error.
|