| |
Flame Quenching in SI Engines
Photographic studies of flame region in a spark ignition engine immediately after arrival of flame close to the combustion chamber walls have shown existence of a thin non-radiating layer adhering to the combustion chamber. Flame propagates through unburned charge when the energy released on combustion is able to maintain the reaction zone temperatures at a high enough level to sustain the rapid combustion reactions. However, as the flame approaches combustion chamber walls, more and more heat is lost from the flame to the walls. Due to heat transfer from the flame to the walls, temperature of the reaction zone gets lowered that slows down combustion reactions reducing heat release rate. Finally, as the flame reaches in close proximity of the walls, the gas temperature ahead of flame falls below ignition point and the flame gets extinguished. This phenomenon is known as flame quenching.
The flame propagating normal to the single wall will quench at some distance away. When the flame is propagating through a tube it may not propagate if the tube diameter is smaller than a critical value. Similarly, flame may not propagate between the two parallel plates if the distance between the plates is below a critical limit. The normal distance from the wall where flame gets quenched, or the gap between two parallel plates, or diameter of the tube in which flame is just unable to propagate under the given charge conditions, is called quench distance or quench layer thickness. The wall-quenching effects are primarily due to heat transfer and not due to diffusion of species.
Quench Layer Thickness
Let us consider that flame is propagating normal to a single wall.
At the Instant of Flame Quenching |
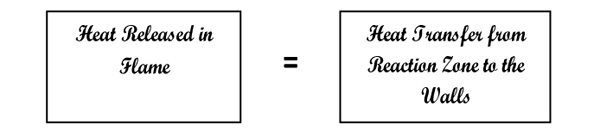 |
For a laminar flame and also as the flame is very close to the walls, heat from the reaction zone is mainly transferred by conduction and, the convection effects may be neglected. Thus,
where
k |
= |
Thermal conductivity of the unburned mixture, |
|
= |
Characteristic temperature difference for heat transfer, |
|
= |
Quench distance, |
|
= |
Unburned mixture density, |
|
= |
Laminar flame speed, |
h |
= |
Heat release per unit mass of the mixture burned, |
|
= |
Average specific heat of burned gases, and |
|
= |
Temperature rise on combustion in the flame. |
Introducing thermal diffusivity, a in the equation 6.39, we get
A similar relationship for the flame quenching between two parallel plates is also obtained. The dimensionless quantity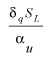 is Peclet number. is Peclet number.
|