Polynomial-fitting Approach:
By assuming a polynomial variation of the field variable in the neighborhood of the point of interest, it is possible to obtain the difference expressions for the derivatives. For instance, 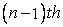 degree polynomial can be fitted between n nodes, for the field variable and this polynomial can be used for evaluating upto the degree polynomial can be fitted between n nodes, for the field variable and this polynomial can be used for evaluating upto the 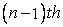 derivative. derivative.
Using two points, say i and i+1 , a linear variation can be assumed for the variable 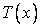 and this leads to and this leads to
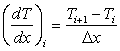 |
(6.6) |
For linear variation between i and 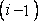
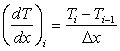 |
(6.7) |
Similarly, the central difference expression
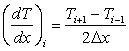 |
(6.8) |
can be obtained by using a linear variation between 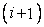 and and 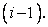
For parabolic variation between points, 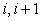 and and 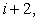 one can set: one can set:
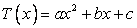 |
(6.9) |
where , a, b, c, are obtained from
In matrix form,
Inversion of Eqn. (6.13) leads to the values of a, b, c in terms of 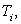 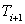 and and 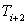 . Having obtained the values of these coefficients, the derivative . Having obtained the values of these coefficients, the derivative 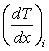 can be evaluated as: can be evaluated as:
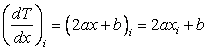
|
(6.14) |
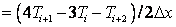 |
|
where,
The second derivative at i can also be evaluated from the polynomial expression of (2.32) and this is given by:
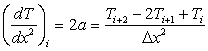 |
(6.15) |
The polynomial fitting procedure can thus be extended for obtaining difference expressions for higher order derivatives also. By considering 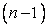 neighboring point in addition to i, derivatives upto neighboring point in addition to i, derivatives upto 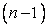 th order can be calculated. The polynomial fitting technique is very useful when the boundary conditions of the problem are of a very complex nature and involve various derivatives of the unknown dependent variable. th order can be calculated. The polynomial fitting technique is very useful when the boundary conditions of the problem are of a very complex nature and involve various derivatives of the unknown dependent variable.
Congratulations! You have finished Lecture 6. To view the next lecture select it from the left hand side menu of the page or click the next button.
|