ADI Method

The difficulties described in the earlier section, which occur when solving the two-dimensional equation by conventional algorithms, can be removed by alternating direction implicit (ADI) methods. The usual ADI method is a two-step scheme given by

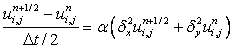(6.1)

and

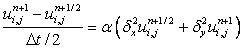(6.2)

The effect of splitting the time step culminates in two sets of systems of linear algebraic equations. During step 1, we get the following

or

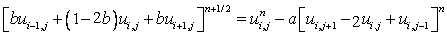(6.3)

Now for each “j” rows( j = 2,3...)we can formulate a tridiagonal matrix, for the varying i index and obtain the values from i=2 to (imax-1) at (n+1/2) level Fig.6.1 (a).

Figure 6.1(a)

Similarly, in step-2, we get

or

Now for each “i” rows ( i = 2,3...) we can formulate a tridiagonal matrix for the varying j index and obtain the values from j =2 to (jmax-1) at nth level Fig. 2.5 (b).