The resulting system of linear algebraic equations is not tridiagonal because of the five unknowns 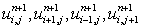 and and 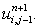 In order to examine this further, let us rewrite Eq. (5.7) as In order to examine this further, let us rewrite Eq. (5.7) as
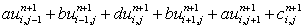 |
(5.9) |
where
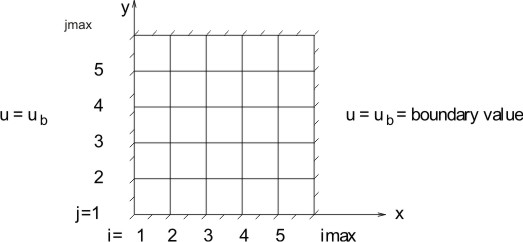
Figure 5.2: Two-dimensional grid on the ( 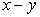 ) plane. ) plane.
Eq. (5.9) can be applied to the two-dimensional (6×6) computational grid shown in Fig. 5.2.
A system of 16 linear algebraic equations have to be solved at 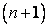 time level, in order to get the temperature distribution inside the domain. The matrix equation will be as the following: time level, in order to get the temperature distribution inside the domain. The matrix equation will be as the following:
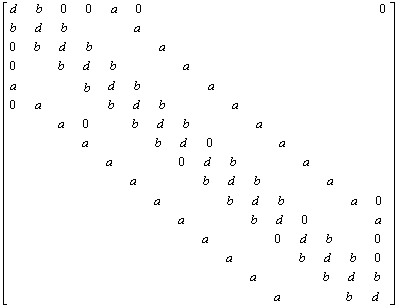 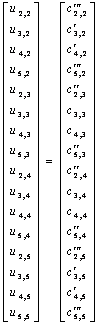 |
(5.9) |
where
The system of equations, described by Eq. (5.9) requires substantially more computer time as compared to a tridiagonal system. The equations of this type are usually solved by iterative methods. These methods will be described in a subsequent lecture. The quantity 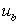 is the boundary value. is the boundary value.
Congratulations! You have finished Lecture 5. To view the next lecture select it from the left hand side menu of the page or click the next button.
|