| |
Calculation of Pressure
The method of pressure calculation can be derived from the SIMPLE algorithm of Patankar and Spalding (1972). A detailed description can be found in Peric (1985) and Ferziger and Peric (1999).
The velocity field obtained by solving the discretized form of the momentum equation (37.2) does not necessarily satisfy mass conservation. To check this, the mass fluxes through the CV faces (Eq. (37.14)) have to be calculated, requiring the evaluation of the velocity components at CV face locations “e”, “w”, “n”, and “s”. The method employed for the momentum equations, are not suitable for this purpose, since oscillatory pressure fields may then result from the SIMPLE algorithm. An interpolation practice which avoids this problem has been suggested by Patankar and successfully used by Hsu (1981), Rhie and chow (1983) and Peric (1985). The discretized momentum equations serve as the basis for this interpolation. Equations (39.12) can , for this purpose, be rewritten as follows:
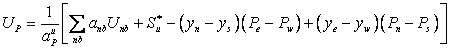 |
(41.1) |
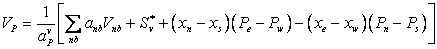 |
here the pressure terms are excluded from 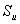 and and 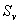 and written explicitly, leaving the rest of the source terms as and written explicitly, leaving the rest of the source terms as 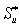 and and 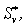 respectively. To obtain the velocity at the “e”-cell face (Fig. 41.1), the terms on the right hand side of Eq. (41.1) are interpolated individually. All terms except the pressure difference across the cell face are interpolated linearly, using CDS expressions (40.1). respectively. To obtain the velocity at the “e”-cell face (Fig. 41.1), the terms on the right hand side of Eq. (41.1) are interpolated individually. All terms except the pressure difference across the cell face are interpolated linearly, using CDS expressions (40.1).
|