Consistency
A finite difference representation of a partial differential equation (PDE) is said to be consistent if we can show that the difference between the PDE and its finite difference (FDE) representation vanishes as the mesh is refined, i.e,
| lim (PDE-FDE) = |
lim (TE)=0 |
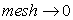 |
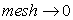 |
A questionable scheme would be one for which the truncation error is 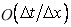 and not explicitly and not explicitly 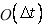 or or 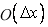 or higher orders. or higher orders.
In such cases the scheme would not be formally consistent unless the mesh were refined in a manner such that 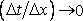 . Let us take Eq. (3.3) and use the Dufort-Frankel (1953) differencing scheme. The FDE is . Let us take Eq. (3.3) and use the Dufort-Frankel (1953) differencing scheme. The FDE is
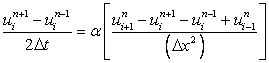 |
(4.1) |
Now the leading terms of truncated series form the truncation error for the complete equation:
The above expression for truncation for error is meaningful if 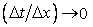 together with together with 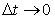 and and 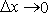 .However, .However,  and and 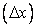 may individually approach zero in such a way that may individually approach zero in such a way that  . Then if we reconstitute the PDE from FDE and TE, we shall obtain . Then if we reconstitute the PDE from FDE and TE, we shall obtain
| lim (PDE-FDE) = |
lim (TE) = |
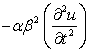 |
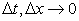 |
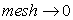 |
And finally PDE becomes
We started with a parabolic one and ended with a hyperbolic one!
So, DuFort-Frankel scheme is not consistent for the 1D unsteady state heat conduction equation unless 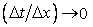 together with together with 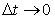 and and 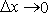 . .
|