The stresses 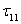 and and 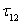 contain velocity derivatives with respect to Cartesian coordinates, see Eq. (37.7); these have to be expressed in terms of general coordinates contain velocity derivatives with respect to Cartesian coordinates, see Eq. (37.7); these have to be expressed in terms of general coordinates 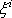 .The quantities .The quantities 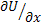 and and 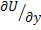 become become
|
(38.1) |
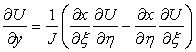 |
Where J is the Jacobian of the coordinate transformation 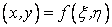 defined by: defined by:
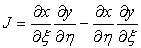 |
(38.2) |
The Jacobian and the derivatives of Eq. (38.1) need to be evaluated at the cell face locations e and n (Fig 37.1). The relations for the e-face will be derived in the following text. The remaining equations follow by analogy.
For the e face, the 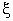 coordinate refer Fig 37.1 is taken to connect the points P and E (from P to E), and coordinate refer Fig 37.1 is taken to connect the points P and E (from P to E), and 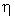 runs along the e cell face (form se to ne). The derivatives runs along the e cell face (form se to ne). The derivatives 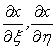 etc., can be approximated as (refer Fig. 37.1): etc., can be approximated as (refer Fig. 37.1):
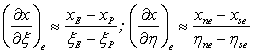 |
(38.3) |
The origin of the 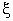 and and 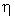 coordinates can be defined as desired. We can calculate coordinates can be defined as desired. We can calculate 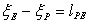 i.e the distance between points P and E; similarly, i.e the distance between points P and E; similarly, 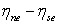 is set equal to is set equal to 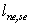 i.e. the length of the cell face between vertices i.e. the length of the cell face between vertices 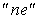 and and 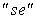 . The Jacobian can then be approximated by: . The Jacobian can then be approximated by:
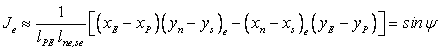 |
(38.4) |
Thus for an orthogonal grid 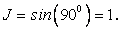 The derivatives in Eqs. (38.1) can now be expressed by involving expressions (38.3) and (38.4) to yield: The derivatives in Eqs. (38.1) can now be expressed by involving expressions (38.3) and (38.4) to yield:
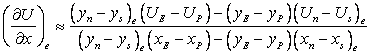
|
(38.5) |
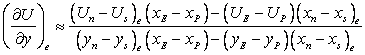 |
The denominator in the above expressions represents the volume defined by the scalar product of 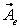 and and 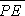 . This will be denoted as . This will be denoted as 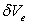 hereafter. hereafter.
|