Consider the weak conservative form of the nondimensional momentum equation in the x- direction:
It is assumed that at 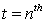 level, we have a coverged solution. Then for the next time step level, we have a coverged solution. Then for the next time step
or
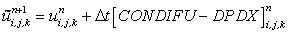 |
(31.1) |
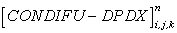 consists of convective and diffusive terms, and the pressure gradient. Similarly, the provisional values for consists of convective and diffusive terms, and the pressure gradient. Similarly, the provisional values for 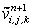 and and 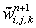 can be explicitly computed. These explicitly advanced velocity components may not constitute a realistic flow field. A divergence-free velocity field has to exist in order to describe a plausible incompressible flow situation. Now, with these provisional can be explicitly computed. These explicitly advanced velocity components may not constitute a realistic flow field. A divergence-free velocity field has to exist in order to describe a plausible incompressible flow situation. Now, with these provisional 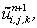 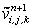 and and 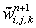 values, continuity equation is evaluated in each cell. If values, continuity equation is evaluated in each cell. If 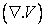 produce a nonzero value, there must be some amount of mass accumulation or annihilation in each cell which is not physically possible. Therefore the pressure at any cell is directly linked with the value of the produce a nonzero value, there must be some amount of mass accumulation or annihilation in each cell which is not physically possible. Therefore the pressure at any cell is directly linked with the value of the 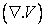 of that cell. Now, on one hand the pressure has to be calculated with the help of the nonzero divergence value and on the other, the velocity components have to be adjusted. The correction procedure continues through an iterative cycle until the divergence-free velocity field is ensured. Details of the procedure will be discussed in the subsequent section. of that cell. Now, on one hand the pressure has to be calculated with the help of the nonzero divergence value and on the other, the velocity components have to be adjusted. The correction procedure continues through an iterative cycle until the divergence-free velocity field is ensured. Details of the procedure will be discussed in the subsequent section.
6. Boundary conditions applied after each explicit evaluation for the time step is accomplished. Since the governing equations are elliptic in space, boundary conditions on all confining surface are required. More over, the boundary conditions are also to be applied after every pressure-velocity iteration.
The five principal kinds of boundary condition to be considered are
- rigrid no-slip walls,
- free-slip walls
- inflow boundaries
- outflow boundaries, and
- periodic (repeating) boundaries.
Congratulations, you have finished Lecture 31. To= view the next lecture select it from the left hand side menu of the page or click the next button. |